전 가산기(Full adder)
가산기(Adder)에는 반가산기(Half adder)와 전가산기(Full adder) 두개가 있다는걸 전 포스트에서 알아보았다.
그 중 전가산기에 대해 알아보자.
앞에서 반가산기는 2개의 2진수 A와 B를 더하여 합(Sum)과 캐리(Carry)를 산출하기 위한 조합 논리회로라는걸 알아 보았다.
그럼 전가산기는 무엇인가?
컴퓨터 내부에서 여러 비트로 된 두 수를 더할 때에는 두 비트에서 더해진 결과인 캐리는
더 높은 자리의 두 비트의 덧셈에 추가되어 더해진다.
이때, 아래 자릿수에서 발생한 캐리까지 포함하여 세 비트를 더하는 논리회로를 전가산기(Full adder)라고 한다.
따라서 전가산기는 3개의 입력을 갖는다.
전가산기의 진리표는 아래와 같다.
이 진리표를 가지고 S 와 C의 각각 카르노 맵을 작성해보면 아래와 같다.
바로 아래는 S(Sum)의 카르노맵이다.
이 카르노맵에서는 인접된 항이 없으므로, 다음과 같이 불 대수 정리를 이용하여 간소화 한다.
S = X'Y'Z + X'YZ' + XY'Z' + XYZ
= X'(Y'Z + YZ') + X(Y'Z' + YZ)
= X'(Y ![]() Z) + X(Y⊙Z)
Z) + X(Y⊙Z)
= X'(Y 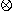 Z) + X(Y
Z) + X(Y 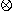 Z)'
Z)'
= X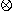 (Y
(Y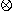 Z)
Z)
= X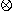 Y
Y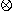 Z
Z
따라서 S의 논리식은 S = X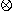 Y
Y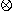 Z 이다.
Z 이다.
또 바로 아래는 C(Carry)의 카르노맵이다.
Carry 카르노맵은 인접된 항이 존재하여 위와같이 묶어준다.
따라서 Carry의 논리식은 아래와 같다.
C = XY + XZ + YZ
자 S 와 C의 논리식을 가지고 논리회로를 그려보자.
순수하게 AND와 OR, NOT 인 기본게이트로만 이루어진 논리회로는 아래와 같다.
(그림1)
Z는 입력이므로 Cin으로 대체한 기본게이트로 이루어진 전가산기의 논리회로이다.
하지만 간소화를 거친뒤 줄일수 있는데로 줄이고 회로를 XOR 형식으로 바꾸면 아래와 같이 나온다.
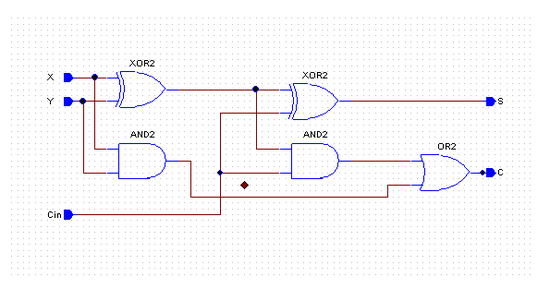
(그림 2)
어떤가? '그림1' 보다 '그림2' 가 더 간편해 보이는걸 눈으로 확인이 가능하다.
당연히 '그림1'의 논리회로가 '그림2'의 논리회로보다 비용이 더들고 복잡하다는걸 알 수 있다.
따라서 가장 최적화되고 전가산기에있어 가장 획기적인 회로설계 방식은 '그림2'와 같다고 볼 수 있다.
Hidden TIP) 자세히 보면 반가산기가 2개 있다는걸 알 수 있다. ^^
하지만 반가산기에서도 그랬듯이 먼저 XOR을 이용한 논리회로 방식을 처음부터 그리는것 보단
'그림1'처럼 간소화 전 기본게이트로 한번 그려보고 원리를 이해한 뒤 그다음 '그림2'를 그려봐야 한다.
아래는 가산기를 응용한 2진병렬 가산기회로이다. 참고하길 바란다.
참조 : http://blog.naver.com/asd7979?Redirect=Log&logNo=30108134761
'[알고리즘]' 카테고리의 다른 글
| LHS 변수 와 RHS 변수 란 무엇인가? (0) | 2013.04.03 |
|---|---|
| [MATLAB] matlab source code를 EXE 파일로 변환하기 (0) | 2013.03.29 |
| 조합 논리회로 (Combination Logic Circuit) : 반가산기 (0) | 2013.03.28 |
| MSB(Most Significant Bit)/LSB(Least Significant Bit)란 무엇인가? (0) | 2013.01.14 |
| 영역처리 : 외곽선 검출(Edge Detecting) (0) | 2012.11.08 |



